Ncert Exempler Class lX Circles

 CIRCLES

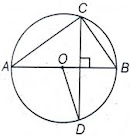
1. In Fig., O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.

2. AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q² = p² + 3r² .

3.In Fig. 10.19, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = 1/ 2 (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).

4. ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.

5. If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.

6. In Fig. , ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

7. A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.

8. Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′. 

9. If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic

10. Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle