class lX ncert Heron's formula

 Heron's formula

1. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm

2. The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.

3. : Kamla has a triangular field with sides 240 m, 200 m, 360 m, where she grew wheat. In another triangular field with sides 240 m, 320 m, 400 m adjacent to the previous field, she wanted to grow potatoes and onions (see Fig). She divided the field in two parts by joining the mid-point of the longest side to the opposite vertex and grew patatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions?

4. Students of a school staged a rally for cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes AB, BC and CA; while the other through AC, CD and DA (see Fig.). Then they cleaned the area enclosed within their lanes. If AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m and ∠ B = 90º, which group cleaned more area and by how much? Find the total area cleaned by the students (neglecting the width of the lanes).

5, Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

6. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

7. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig.), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella? 

8. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. . How much paper of each shade has been used in it? 

9. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. ). Find the cost of polishing the tiles at the rate of 50p per cm² .

Class Xl Ncert Probability

 PROBABILITY

1. A coin is tossed. If it shows head, we draw a ball from a bag consisting of 3 blue and 4 white balls; if it shows tail we throw a die. Describe the sample space of this experiment.

2. An experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occurs on the first toss, then a die is rolled once. Find the sample space.

3.The numbers 1, 2, 3 and 4 are written separatly on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Describe the sample space for the experiment.

4. The numbers 1, 2, 3 and 4 are written separatly on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Describe the sample space for the experiment.

5. A die is thrown repeatedly untill a six comes up. What is the sample space for this experiment?

6. Consider the experiment of rolling a die. Let A be the event ‘getting a prime number’, B be the event ‘getting an odd number’. Write the sets representing the events (i) Aor B (ii) A and B (iii) A but not B (iv) ‘not A’.

7. Two dice are thrown and the sum of the numbers which come up on the dice is noted. Let us consider the following events associated with this experiment

 A: ‘the sum is even’. 

B: ‘the sum is a multiple of 3’. 

C: ‘the sum is less than 4’. 

D: ‘the sum is greater than 11’. 

Which pairs of these events are mutually exclusive?

8. Three coins are tossed once. Let A denote the event ‘three heads show”, B denote the event “two heads and one tail show”, C denote the event” three tails show and D denote the event ‘a head shows on the first coin”. Which events are (i) mutually exclusive? (ii) simple? (iii) Compound?

9. Two dice are thrown. The events A, B and C are as follows: A: getting an even number on the first die. B: getting an odd number on the first die. C: getting the sum of the numbers on the dice ≤ 5. Describe the events (i) A′  (ii)  not B   (iii) A or B   (iv) A and B    (v) A but not C    (vi) B or C          (vii) B and C    (viii) A ∩ B′ ∩ C′

10. A bag contains 9 discs of which 4 are red, 3 are blue and 2 are yellow. The discs are similar in shape and size. A disc is drawn at random from the bag. Calculate the probability that it will be (i) red, (ii) yellow, (iii) blue, (iv) not blue, (v) either red or blue

11. Two students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that 

(a) Both Anil and Ashima will not qualify the examination. 

(b) Atleast one of them will not qualify the examination and 

(c) Only one of them will qualify the examination.

12. A committee of two persons is selected from two men and two women. What is the probability that the committee will have (a) no man? (b) one man? (c) two men?

13. A card is selected from a pack of 52 cards. (a) How many points are there in the sample space? (b) Calculate the probability that the card is an ace of spades. (c) Calculate the probability that the card is (i) an ace (ii) black card.

14. A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up. 

From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.

15. If 2/11  is the probability of an event, what is the probability of the event ‘not A’.

16. In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?

17. 5 Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains (i) all Kings (ii) 3 Kings (iii) atleast 3 Kings. 

18. If A, B, C are three events associated with a random experiment, prove that 

P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) -P(A∩C)-P(B∩C) + P(A∩B∩C)

19. The number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?

20. Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope.

Ncert Exempler Class lX Circles

 CIRCLES

1. In Fig., O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.

2. AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q² = p² + 3r² .

3.In Fig. 10.19, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = 1/ 2 (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).

4. ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.

5. If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.

6. In Fig. , ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

7. A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.

8. Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′. 

9. If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic

10. Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle

NCERT Exempler class Vlll Comparing Qunatity

 Comparing Quantity

1. Vishakha offers a discount of 20% on all the items at her shop and still makes a profit of 12%. What is the cost price of an article marked at Rs 280?

2. A TV set was bought for Rs 26,250 including 5% VAT. find The original price of the TV ?

3. Radhika bought a car for Rs 2,50,000. Next year its price decreased by 10% and further next year it decreased by 12%. In the two years overall decrease per cent in the price of the car is

4. In a factory, women are 35% of all the workers, the rest of the workers being men. The number of men exceeds that of women by 252. Find the total number of workers in the factory

5. In the year 2001, the number of malaria patients admitted in the hospitals of a state was 4,375. Every year this number decreases by 8%. Find the number of patients in 2003

6. Babita bought 160 kg of mangoes at Rs 48 per kg. She sold 70% of the mangoes at Rs 70 per kg and the remaining mangoes at Rs 40 per kg. Find Babita’s gain or loss per cent on the whole dealing.

7. Find the difference between Compound Interest and Simple Interest on Rs 45,000 at 12% per annum for 5 years.

8. A new computer costs Rs 1,00,000. The depreciation of computers is very high as new models with better technological advantages are coming into the market. The depreciation is as high as 50% every year. How much will the cost of computer be after two years?

9. Lemons were bought at Rs 48 per dozen and sold at the rate of Rs 40 per 10. Find the gain or loss per cent.

10. Ashima sold two coolers for Rs 3,990 each. On selling one cooler she gained 5% and on selling the the other she suffered a loss of 5%. Find her overall gain or loss % in whole transaction.

11. A lady buys some pencils for Rs 3 and an equal number for Rs 6. She sells them for Rs 7. Find her gain or loss%.

12. On selling a chair for Rs 736, a shopkeeper suffers a loss of 8%. At what price should he sell it so as to gain 8%?

13. What price should a shopkeeper mark on an article that costs him Rs 600 to gain 20%, after allowing a discount of 10%

14. Given the principal = Rs 40,000, rate of interest = 8% p.a. compounded annually. Find 

(a) Interest if period is one year. 

(b) Principal for 2nd year. 

(c) Interest for 2nd year. 

(d) Amount if period is 2 years

ncert exempler class lX quadrilateral

. • Sum of the angles of a quadrilateral is 360º, 

• A diagonal of a parallelogram divides it into two congruent triangles,

 • In a parallelogram (i) opposite angles are equal (ii) opposite sides are equal (iii) diagonals bisect each other. 

• A quadrilateral is a parallelogram, if (i) its opposite angles are equal (ii) its opposite sides are equal (iii) its diagonals bisect each other (iv) a pair of opposite sides is equal and parallel. 

• Diagonals of a rectangle bisect each other and are equal and vice-versa • Diagonals of a rhombus bisect each other at right angles and vice-versa 

• Diagonals of a square bisect each other at right angles and are equal and vice-versa 

• The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it

• A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side, 

• The quadrilateral formed by joining the mid-points of the sides of a quadrilateral, taken in order, is a parallelogram.

1.The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.

2. E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram

3. E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC.

4. D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆ DEF is also an equilateral triangle

5. Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Fig. ). Show that AC and PQ bisect each other.

6. Show that the quadrilateral formed by joining the mid-points the sides of a rhombus, taken in order, form a rectangle.

7. A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.

8. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.

9. P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.

10. AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF

   

11. P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram. 

12. ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.

13. P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.

14. D, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent triangles.

15. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = ½ (AB + CD).

class lX Surface area and Volume (part 2)

 Volume of a Cuboid = base area × height = length × breadth × height

Volume of a Cube = edge × edge × edge = a ³

Volume of a Cylinder = πr ²h

Volume of a Cone = 1/3 πr ²h

Volume of a Sphere = 4/ 3 3 πr³

Volume of a Hemisphere = 2/3 3 πr³

IMPORTANT QUESTIONS

1. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S′. Find the (i) radius r′ of the new sphere, (ii) ratio of S and S′.

2. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?

3. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³ ) is needed to fill this capsule?

4. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?

5. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.

6. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?

7. The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?

8. The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm³ of wood has a mass of 0.6 g.

9. At a Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses  of radius 3 cm up to a height of 8 cm, and sold for Rs.15 each. How much money does the stall keeper receive by selling the juice completely?

10. A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas. 

11. A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?

12. The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.

13. A godown measures 40 m × 25 m × 15 m. Find the maximum number of wooden crates each measuring 1.5 m × 1.25 m × 0.5 m that can be stored in the godown.

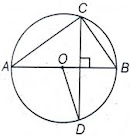
class lX circles

 Circles

1. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.

2. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.

3.Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?

4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see fig)

5. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

6.: Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.

7. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

8. In Fig. , ∠ ABC = 69°, ∠ ACB = 31°, find ∠ BDC.

9. In Fig. , A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠ BAC.

10. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

11. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig.). Prove that ∠ACP = ∠ QCD.

12. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

class Vlll Comparing Quantities

 Comparing Quantities

1. If Chameli had Rs 600 left after spending 75% of her money, how much did she have in the beginning? 

2.Convert the following ratios to percentages. (a) 3 : 4 

3.  A shopkeeper purchased 200 bulbs for Rs10 each. However 5 bulbs were fused and had to be thrown away. The remaining were sold at ` 12 each. Find the gain or loss %.?

4. The cost of an article was Rs15,500. Rs 450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.

5. A VCR and TV were bought for ` 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss percent on the whole transaction.

6. A milkman sold two of his buffaloes for ` 20,000 each. On one he made a gain of 5% and on the other a loss of 10%. Find his overall gain or loss.

7. An article was purchased for ` 1239 including GST of 18%. Find the price of the article before GST was added?

8. Kamala borrowed Rs 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?

9. Maria invested Rs 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find

 (i) The amount credited against her name at the end of the second year. 

(ii) The interest for the 3rd year.

10. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum 

(i) find the population in 2001.

 (ii) what would be its population in 2005? 

11. In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5, 06,000. 

12. A scooter was bought at Rs 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.

class Vlll Cubes and Cube roots

 Cubes and Cube Roots

 1.  Is 392 a perfect cube? If not, find the smallest natural number by which 392 must be multiplied so that the product is a perfect cube.

2. Is 53240 a perfect cube? If not, then by which smallest natural number should 53240 be divided so that the quotient is a perfect cube?

3. Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?

4. Find the cube root of 8000?

5. You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.

credit: ncert.nic.in

class IX Quadrilateral

 

QUADRILATERALS

1.Two parallel lines l and m are intersected by a transversal p (see Fig.). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.

 

 

2.Show that the bisectors of angles of a parallelogram form a rectangle.

3.Show that if the diagonals of a quadrilateral are equal and bisect each other at right.

 

4.In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. ). Show that:

(i)               

∆ APD ≅ ∆ CQB

(ii)              AP = CQ

(iii)            ∆ AQB ≅∆ CPD

(iv)            AQ = CP

(v)              APCQ is a parallelogram

5. In ∆ ABC and ∆ DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig.). Show that

(i)               

quadrilateral ABED is a parallelogram

(ii)              quadrilateral BEFC is a parallelogram

(iii)             AD || CF and AD = CF

(iv)             quadrilateral ACFD is a parallelogram

(v)               AC = DF

(vi)            ∆ ABC ≅ ∆ DEF.

 

6. ABCD is a trapezium in which AB || CD and AD = BC (see Fig.). Show that

 (i) ∠ A = ∠ B

 (ii) ∠ C = ∠ D

(iii) ∆ ABC ≅ ∆ BAD

 (iv) diagonal AC = diagonal BD

7. l, m and n are three parallel lines intersected by transversals p and

 q such that l, m and n cut off equal intercepts AB and BC on p (see

 Fig.). Show that l, m and n cut off equal intercepts DE and EF on q

 also

 

 

 

 

 

8. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig). AC is a diagonal. Show that:

(i)               

SR || AC and SR = 1/ 2 AC

(ii)              PQ = SR

(iii)           PQRS is a parallelogram.

 

 

 

9. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

 

10. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig.). Show that the line segments AF and EC trisect the diagonal BD.

                                                             

 

 

 

 11. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that

(i)                D is the mid-point of AC

(ii)             MD ⊥AC

(iii)           CM = MA = 1 /2 AB